Differential ideal
In the theory of differential forms, a differential ideal I is an algebraic ideal in the ring of smooth differential forms on a smooth manifold, in other words a graded ideal in the sense of ring theory, that is further closed under exterior differentiation d. In other words, for any form α in I, the exterior derivative dα is also in I.
In the theory of differential algebra, a differential ideal I in a differential ring R is an ideal which is mapped to itself by each differential operator.
Exterior differential systems and partial differential equations
An exterior differential system on a manifold M is a differential ideal
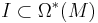 .
.
One can express any partial differential equation system as an exterior differential system with independence condition. Say that we have kth order partial differential equation systems for maps 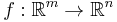 , given by
, given by
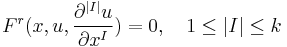 .
.
The solution of this partial differential equation system is the submanifold  of the jet space consisting of integral manifolds of the pullback of the contact system to
of the jet space consisting of integral manifolds of the pullback of the contact system to  .
.
This idea allows one to analyze the properties of partial differential equations with methods of differential geometry. For instance, we can apply Cartan's method on partial differential equation systems by writing down the exterior differential system associated with it.
Perfect differential ideals
a differential ideal 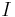 which has the property that if it contains an element
which has the property that if it contains an element 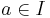 they contain any element
they contain any element 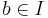 such that
such that 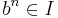 for some
for some 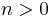 is equal to
is equal to 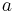 .
.
References
- Bryant, Phillip Griffiths and Lucas Hsu, Toward a geometry of differential equations(DVI file), in Geometry, Topology, & Physics, Conf. Proc. Lecture Notes Geom. Topology, edited by S.-T. Yau, vol. IV (1995), pp. 1–76, Internat. Press, Cambridge, MA
- Oleg I. Morozov, Structure of Symmetry Groups via Cartan's Method: Survey of Four Approaches(PDF file), SIGMA, Vol. 1 (2005), Paper 006, 14 pages; math-ph/0508016
- H. W. Raudenbush, Jr. "Ideal Theory and Algebraic Differential Equations", Transactions of the American Mathematical Society, Vol. 36, No. 2. (Apr., 1934), pp. 361-368. Stable URL:[1]